A useful way of dealing with a Bezier curve is to split it into two curves. I’ve found a nice way to do that and will record it here. Advanced recipe? Weird.
Source
I’ve found a number of references on how to do what we’ll do here today. This article includes the answer that I’m recording here, because the article nicely shows how simple it is to do the job.
Motivation
For Valkyrie Transport’s purposes, we need to follow paths in terms of distance along the path. While Bezier curves make for nice smooth motion, it is not possible to directly determine the Bezier parameter, t, that corresponds to a distance d. One has to make multiple evaluations. That takes time, and we’d rather not.
An interesting fact is that while the original control point quadrilateral doesn’t look much like the curve, if you split the curve into two curves, the new control shapes look more like the curve. If you split again, they get closer. In fact, they converge to be exactly the curve, the more you split.
Better yet, for the kind of well-behaved Bezier curves we use at VT, they converge well enough at three splits (8 Beziers), or worst case, four splits (16 Beziers).
So while it would look really wacky if you followed the control quad for the original Bezier, if you split three times and follow those lines, it looks good enough.
We already have code, somewhere in my library and these articles, that divides up the Bezier into N segments by repeated evaluation of equal values of t. And, also somewhere, I have code that finds equal-length segments following a Bezier, although it is quite costly.
Today’s scheme offers another way of getting the equal-t-values split, and it is simple and clear. Which one will we use? I don’t know. It’s early days, we’re just learning
Recipe
Given a Bezier curve with vector control points a, b, c, d, compute
-- just typed in not yet tested
-- starting with Bezier (a, b, c, d)
local e = (a+b)/2
local f = (b+c)/2
local g = (c+d)/2
-- note that the pattern shifts here
local h = (e+f)/2
local i = (f+g)/2
local j = (h+i)/2
return Bezier(a, e, h, j), Bezier(j, i, g, d)
Note that I renamed the last two variables. The original author apparently wanted to avoid the letter “I”. Old FORTRAN programmer perhaps. But then why not skip J and K … ? I don’t know.
Using the recipe
With the split above, we can approximate the curve with the lines between the parameters: a-e-h-j-i-g-d. If we split each of those Beziers again, using the same formula on each, the fit is better. Here’s a picture:
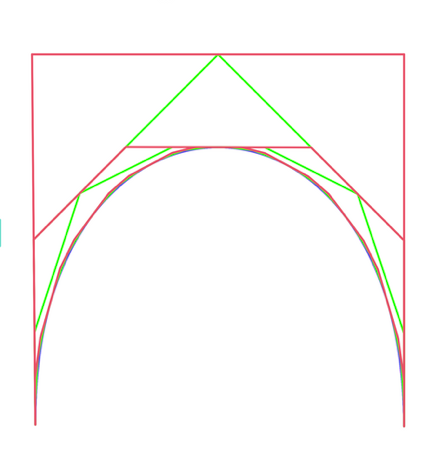
The different colors show some of the splitting. Notice that each split cuts corners off the preceding one and the third split touches the curve at the half-way (t) point. There is also a similar picture in the article linked above. Remember that that article skips the letter “I” and I did not.
In practice, we’ll pick some standard number of splits and convert each Bezier that we generate directly to a series of line segments. After that, we’ll have the total length of that Bezier, the sum of the lengths of the line segments. So it is “easy” to see whether the distance we want to move to is within any given bezier and a quick search to find the segment that corresponds to the distance we want. One quick interpolation and we have the point.
Which way of splitting is best? I’m not sure. I think they produce exactly the same results, one by evaluating the Bezier multiple times at desired values of t, the other splitting the bezier down to the same t value. (We will probably use 1/2, 1/4, 1/8, 1/16 for splits on t. (Well, I suppose one could use 1/3, 1/9 … or anything …))
The choice will come down to whichever method is faster, I suspect. My estimate is that there is plenty of time to compute the segments right when we create the new Bezier from the Guides. If that turns out not to be the case, we can do them incrementally, but we’d prefer not to add that complexity unless we really need to.
Summary
Another way of getting to places we might want to get to. We’re in the process of learning and creating options from which we’ll choose.
Safe paths!