Today we’ll see if we can do the piston rod. We’ll stick with the horizontal version for now. Wish me luck!
The piston rod is pretty simple: it just goes back and forth, typically driven by a connecting rod, which is driven by a drive wheel. It occurs to me, however, that I can test the PistonRod independently. And therefore, I should do that.
“Why?”, you may be asking. Well, for one thing the tests will be much easier to write. Instead of setting up a linkage and figuring out what it’ll do to the piston rod, we’ll just pick some positions for the pushed end, and compute the central position. Since our tests for other objects give us confidence that they’ll produce the right results, we can be confident that, assembled, they’ll get the right results. We’ll still do some “story tests”, as they are called, and we plan to draw some SVG pictures to see our results, so we= wont’ be without tests for assemblies.
It is nearly true that if all the pieces work correctly, the program will work correctly. So if we focus primarily on the pieces al being correct, we’re a very long way toward everything working, without the effort of building more and more complicated tests.
We will need some kind of driver object, of course … at least as things work now, because each linkage piece asks its parent for values, typically position so far. An object built just to support testing is called a “test double”, among other names. They are a bit of a pain to write. Let’s see if we can avoid writing one.
My idea is this: the calculate method, as we have it working now, asks the parent object for whatever info the piece needs, and then computes its own information. We could separate getting the information from using it, which would make testing easier. Let me explain the idea with a refactoring of one of our existing objects.
function ConnectingRod:calculate()
local base_pos = self._parent:position()
local rotated = self._parent:adjusted_offset(self._offset)
local wheel_end = base_pos + rotated
self._position = self:center_position(base_pos, wheel_end)
end
The first two lines access the parent, and the next two do the work. We refactor:
function ConnectingRod:calculate()
local base_pos = self._parent:position()
local rotated = self._parent:adjusted_offset(self._offset)
self:compute_center(base_pos, rotated)
end
function ConnectingRod:compute_center(base_pos, rotated)
local wheel_end = base_pos + rotated
self._position = self:center_position(base_pos, wheel_end)
end
With this form, we can test the actual works without reference to the parent. We’ll leave this code in place, though I do think that the ConnectingRod will benefit from a bit of improvement after this change. But we don’t want to lose sight of this morning’s goal, the PistonRod.
Let’s write a test:
function _:featurePistonRod()
_:describe("horizontal piston rod", function()
_:test("rod center", function()
local rod = PistonRod{parent=666, position=vector(7,2), length=2}
rod:compute_center(vector(5, 2))
_:expect(rod:position()).is(vector(6, 2))
end)
end)
end
The rod is 2 units long, so its center is one unit away from the end. (We have an issue with direction that we’ll need to address. So far we are always assuming x forward. That may not hold up: we’ll find out when we get further along.)
This code cries out for a PistonRod with a compute_center method:
PistonRod = class()
function PistonRod:init(parms)
self._parent = parms.parent or error('expected parent')
self._half_length = (parms.length or error('expected length')) / 2
self._position = parms.position or error('expected position')
end
function PistonRod:compute_center(end_position)
self._position = end_position + vector(self._half_length, 0)
end
function PistonRod:position()
return self._position
end
The test passes, and to be honest, it is enough to make me confident in the compute_center method. How wrong could we get it? We do need a test for calculate, which doesn’t even exist, since it isn’t used yet, so I had no reason to write it.
- Bump in the Road
- Our PistonRod needs to ask whatever pushes it for the position of the pushing point—the end of the ConnectingRod, typically. In general, we’ll need this kind of thing. In our tests so far, of the ConnectingRod and GeneralConnectingRod, we’ve just tested the position of the rod, its center.
-
I’ve really not thought about this yet. Both the CouplingRod and ConnectingRod can be tested without regard to the ends that drive things: we can tell from their root position that they are correct. But we can’t use them that way.
-
Our design is inadequate. No surprise, we only design what we want in the moment, improving the design and code as we discover what we need. So let’s see what the PistonRod wants to ask its parent about.
We’ll just write calculate to see what we need:
function PistonRod:calculate()
end
function PistonRod:compute_center(end_position)
self._position = end_position + vector(self._half_length, 0)
end
Well, it pretty much wants the end position of its parent, doesn’t it? What shall we call that? End position? In the coupling rod and ConnectingRod, we did get a value from the DriveWheel, using a method adjusted_offset that passes in a local offset, basically the starting position of the crank, and the DriveWheel rotates it:
function DriveWheel:adjusted_offset(v)
return v:rotate_2d(self._angle)
end
Time to get off the thinking dime and onto the doing dime. We’ll call it drive_point in the ConnectingRods, just to get a name and code in place:
function PistonRod:calculate()
self:compute_center(self._parent:drive_point())
end
If we were ever to call this it wouldn’t work. I could make it work but I really don’t feel comfortable writing code that I think would work if it were used. It’s time for our story test.
_:test("story test", function()
local wheel = DriveWheel{x=3, y=2}
local con_rod = ConnectingRod{parent=wheel, length=6, radius=1}
local piston_rod = PistonRod{parent=con_rod, position=vector(10,2), length=4}
wheel:move(0)
con_rod:calculate()
piston_rod:calculate()
_:expect(piston_rod:position()).is(vector(12,2))
end)
I’m not certain about those numbers but I think they might be right. MOstlhy I just want to make it compute something sensible. It fails asking for drive_point of the con_rod. No surprise, let’s provide it. I suspect we have already computed it, or nearly so. Here’s the ConnectingRod:
function ConnectingRod:calculate()
local base_pos = self._parent:position()
local rotated = self._parent:adjusted_offset(self._offset)
self:compute_center(base_pos, rotated)
end
function ConnectingRod:compute_center(base_pos, rotated)
local wheel_end = base_pos + rotated
self._position = self:center_position(base_pos, wheel_end)
end
function ConnectingRod:center_position(base_pos, wheel_end)
return wheel_end + self:center_delta(base_pos, wheel_end)
end
function ConnectingRod:center_delta(base_pos, wheel_end)
local delta_y = base_pos.y - wheel_end.y
local delta_x =
- math.sqrt(self._length*self._length - delta_y*delta_y)
return vector(delta_x, delta_y) / 2
end
Right: there in center_delta we have the info we need to compute the driven end, so let’s:
function ConnectingRod:center_delta(base_pos, wheel_end)
local delta_y = base_pos.y - wheel_end.y
local delta_x =
- math.sqrt(self._length*self._length - delta_y*delta_y)
self._driven_end = wheel_end + vector(delta_x, delta_y)
return vector(delta_x, delta_y) / 2
end
function ConnectingRod:driven_end()
return self._driven_end
end
This code needs improvement now as well. But we’re trying to make things work. Then we make them good. Test. This might work.
Ack, I named it wrong, it was supposed to be drive_pooint Fix that up:
function ConnectingRod:drive_point()
return self._driven_end
end
I just love being able to test right after I write a few lines. With that in place my test fails:
Feature: horizontal piston rod
Actual: table[x]=0, Expected: 12.
Test: 'story test'.
horizontal piston rod, 4 Tests: Pass 3, Fail 1, Ignored 0.
OK, I need to check the driven end in my test. I should really have enhanced the ConnectingRod tests to check that.
_:test("story test", function()
local wheel = DriveWheel{x=3, y=2}
local con_rod = ConnectingRod{parent=wheel, length=6, radius=1}
local piston_rod = PistonRod{parent=con_rod, position=vector(10,2), length=4}
wheel:move(0)
con_rod:calculate()
_:expect(con_rod:drive_point()).is(vector(10,2))
piston_rod:calculate()
_:expect(piston_rod:position()).is(vector(12,2))
end)
It comes back as 2, not ten. Oh … we’re missing the length among other things. I think I need to back up and work out the drive_point more carefully. Go to the ConnectingRod tests, add a check:
function _:featureConnectingRod()
_:describe("connecting rod", function()
local wheel
local con_rod
_:setup(function()
wheel = DriveWheel{x=10, y=2}
con_rod = ConnectingRod{parent=wheel, length=6, radius=1}
end)
_:test("initial position", function()
_:expect(con_rod:position()).is(vector(8, 2))
_:expect(con_rod:drive_point()).is(vector(14,2))
end)
...
I don’t see how the position of the con rod gets to be eight with the wheel at ten. Are we assuming that the piston is behind the drive wheel? We must be.
This derails me a bit. I need to ditch all my thinking about the piston rod and dig into the assumptions of the ConnectingRod and such.
Ah. In center_delta we have:
function ConnectingRod:center_delta(base_pos, wheel_end)
local delta_y = base_pos.y - wheel_end.y
local delta_x =
- math.sqrt(self._length*self._length - delta_y*delta_y)
self._driven_end = wheel_end + vector(delta_x, delta_y)
print("full delta", vector(delta_x, delta_y))
return vector(delta_x, delta_y) / 2
end
Note the - on delta_x We are assuming that the ConnectingRod extends rearward. So the x = 5 we’re getting is correct, I think.
OK so in our story test, what does this tell us? We have:
_:test("story test", function()
local wheel = DriveWheel{x=3, y=2}
local con_rod = ConnectingRod{parent=wheel, length=6, radius=1}
local piston_rod = PistonRod{parent=con_rod, position=vector(10,2), length=4}
wheel:move(0)
con_rod:calculate()
_:expect(con_rod:drive_point()).is(vector(10,2))
piston_rod:calculate()
_:expect(piston_rod:position()).is(vector(12,2))
end)
We need to be thinking that the piston is left of the wheel. Let’s redo the numbers:
_:test("story test", function()
local wheel = DriveWheel{x=10, y=2}
local con_rod = ConnectingRod{parent=wheel, length=6, radius=1}
local piston_rod = PistonRod{parent=con_rod, position=vector(6,2), length=4}
wheel:move(0)
con_rod:calculate()
_:expect(con_rod:position(),"con").is(vector(8,2))
_:expect(con_rod:drive_point(),"drive").is(vector(5,2))
piston_rod:calculate()
_:expect(piston_rod:position(),"piston").is(vector(4,2))
end)
The test is wrong. The length is 4, driven end is at 5, half of 4 is 2 5-2 is 3. That’s what the code gets.
_:test("story test", function()
local wheel = DriveWheel{x=10, y=2}
local con_rod = ConnectingRod{parent=wheel, length=6, radius=1}
local piston_rod = PistonRod{parent=con_rod, position=vector(6,2), length=4}
wheel:move(0)
con_rod:calculate()
_:expect(con_rod:position(),"con").is(vector(8,2))
_:expect(con_rod:drive_point(),"drive").is(vector(5,2))
piston_rod:calculate()
_:expect(piston_rod:position(),"piston").is(vector(3,2))
end)
Tests are passing. Commit the code. Now let’s see what we have learned or discovered.
Looking Back
Which way?
I think the biggest discovery is that we need a better way of specifying the direction of things. I suppose that when I first did the ConnectinRod I was thinking of pistons trailing the drive wheels, which is pretty common, probably the usual case. But I think in my SVG drawings, and some of my sketches, I was drawing the connecting rod pointing forward, probably because there was more paper on that side of the card.
Be that as it may, I think we need to have a way to make it very explicit which direction is it from the driven end do the center of our pieces. I’ll have to think about that a bit.
Refactoring
The code for the objects needs refactoring, especially after patching in the driven end notion. We can make it better. But that’s not all …
Explicit points?
A piece of linkage will always be a rigid unchanging object: they don’t shrink or grow. We may want to come up with a convention for identifying key points on a piece, such as the driven end and the drive point, perhaps a pivot point on some objects yet to be devised.
While there are probably only a few ways things will be hooked together, there is no telling what we might want to do in the future, so we would do well to have common nomenclature throughout our objects, so that we can always ask for certain things. Right now position is the only such thing. We’ll probably want rotation or angle, and the need for drive_point or whatever we ultimately call it suggests that we might have the same thing for other objects. Common ideas deserve common names.
Is This OK?
Yes, this is OK. We are discovering how to do linkages, by doing them, looking at what we’ve done, improving it, doing things over. It is the same with drawing, where an artist might do many sketches, and might repaint areas multiple times before abandoning the work.
Some people seem to imagine that it is possible to design a complicated program and then just implement the design. In my view, and according to my mentors, this is flat wrong. We must build the thing to learn how to build the thing.
I found a very nice picture yesterday that describes what we’re doing here:
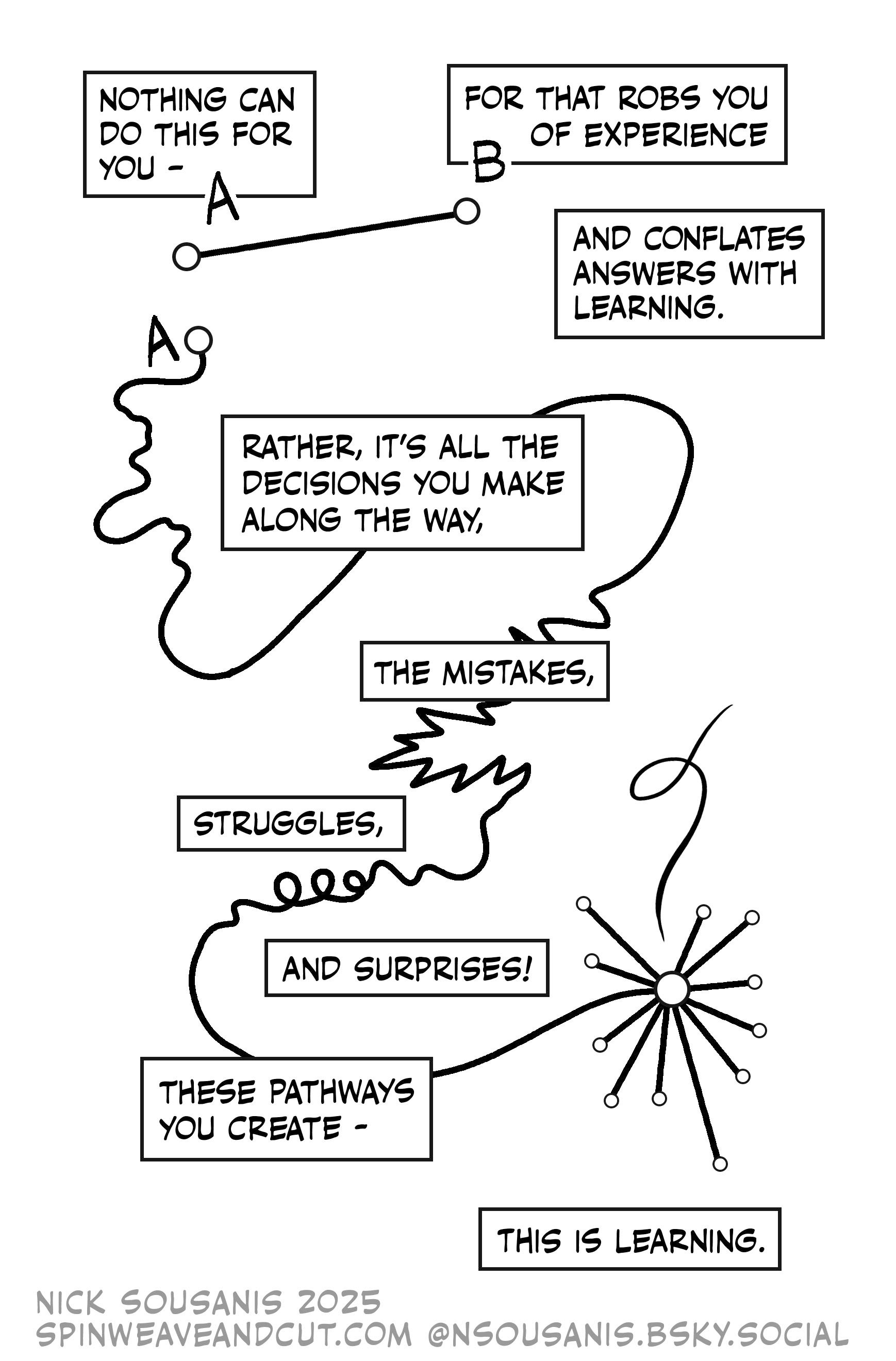
We wander around in the problem and solution, and we learn how to solve the problem and other problems as well. This is the way, er, path.
Safe paths!