The next linkage component that I plan to work on is a link that changes the direction or amount of motion from an input object, typically a main rod or possibly a piston rod. In fact, we don’t care what the input is, we only care about where its effector end is, as is usually the case.
I’ll provide a picture:
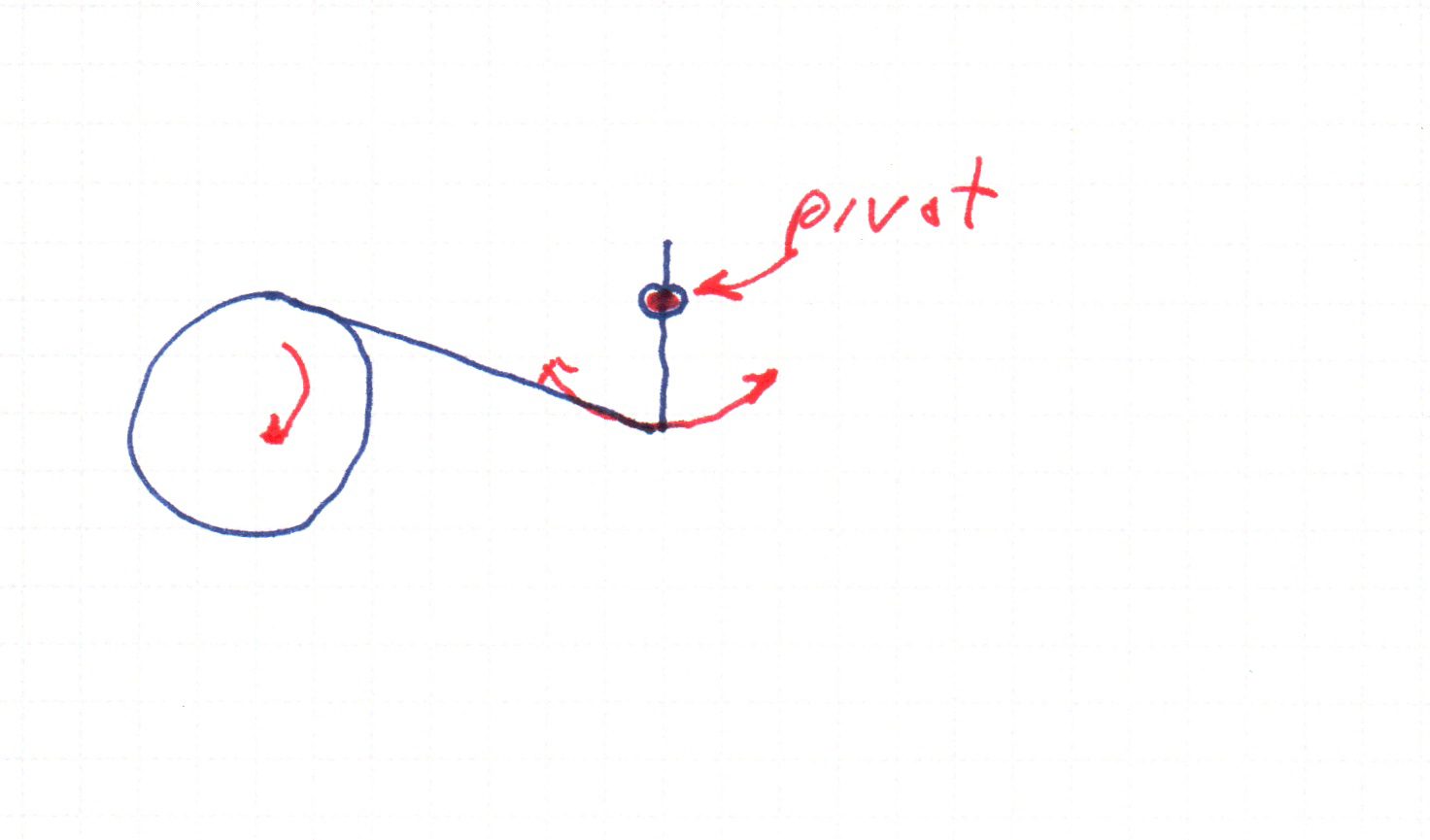
As the drive wheel rotates, the long main rod pushes back and forth. It is connected to the vertical rod, which is pivoted at the indicated point. So the end of the vertical rod is constrained to move in a circular arc. The main rod, of course, has a fixed length. Its start position is somewhere on the drive circle, and we already know how to find that.
When the main rod was connected to a piston rod, the piston rod is constrained to move directly toward or away from the drive wheel center. So we solved for a point on a line whose distance from the starting end of the main rod was its length. With this new situation, we need to solve for a point on a circle, not a line.
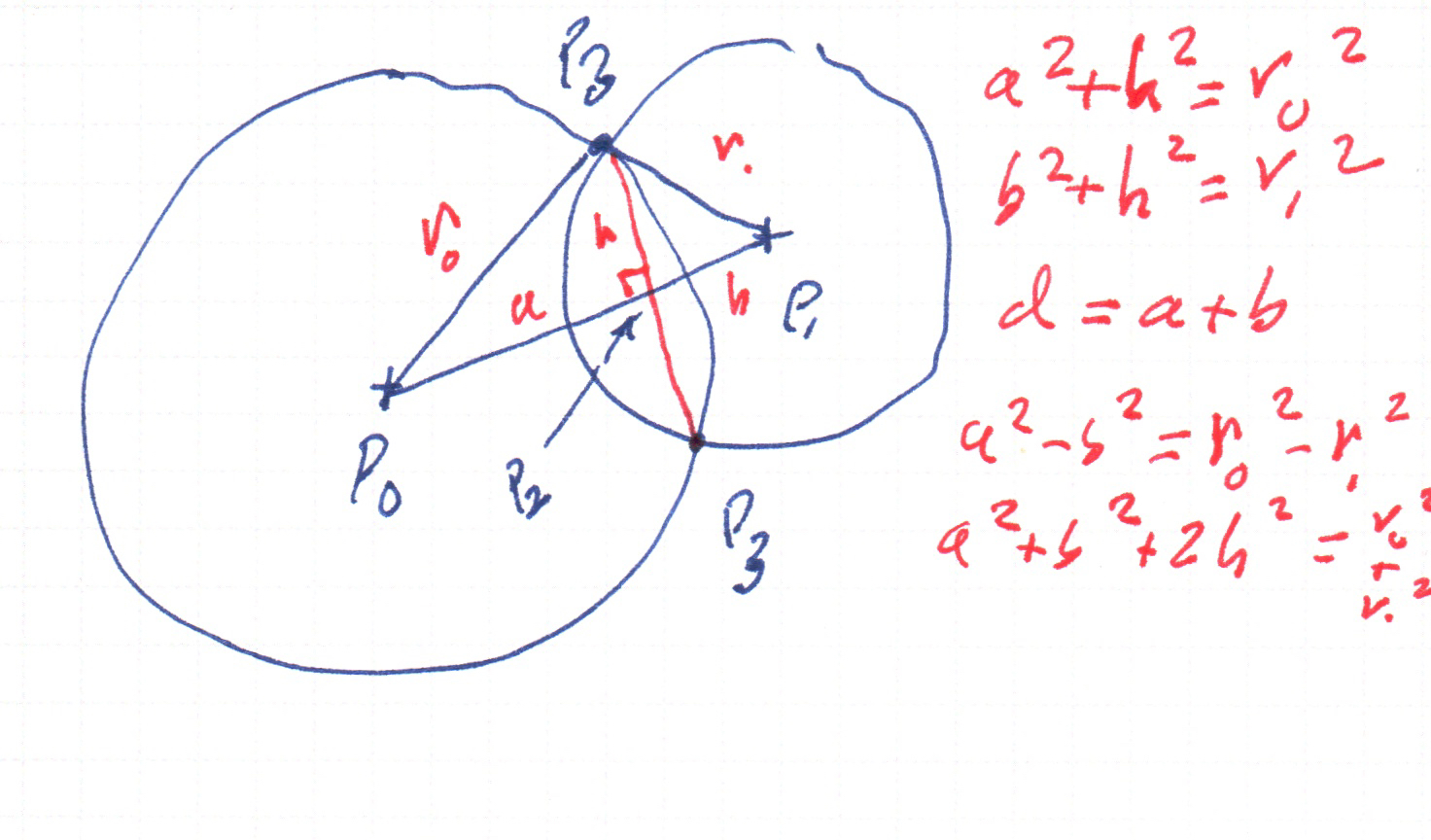
We consider a circle of radius equal to the length of the main rod, and another circle whose radius is the distance from the pivot to the connecting point of the vertical rod. Given the pivot point as the center of the latter circle and the starting point of the main rod as the center of the other circle, the point we want is one of the (generally two) points where the circles intersect.
So, among the things we need is a function to find the intersection points of two circles.
I cheated: I asked Google, and the built-in “AI” thing gave me a decent answer and so I fell into its trap and asked it for some Lua code solving the problem and it provided the code which I’ve put into this test:
local function findCircleIntersection(x0, y0, r0, x1, y1, r1)
local dx = x1 - x0
local dy = y1 - y0
local d = math.sqrt(dx * dx + dy * dy)
-- Check for conditions where no intersection is possible
if d > r0 + r1 or d < math.abs(r0 - r1) or d == 0 then
return nil
end
local a = (r0*r0 - r1*r1 + d*d) / (2 * d)
local h = math.sqrt(r0*r0 - a*a)
local x2 = x0 + a * (x1 - x0) / d
local y2 = y0 + a * (y1 - y0) / d
local x3_1 = x2 + h * (y1 - y0) / d
local y3_1 = y2 - h * (x1 - x0) / d
if h == 0 then
-- Tangent circles, only one intersection point
return { {x = x3_1, y = y3_1}}
end
local x3_2 = x2 - h * (y1 - y0) / d
local y3_2 = y2 + h * (x1 - x0) / d
return { {x = x3_1, y = y3_1}, {x = x3_2, y = y3_2}}
end
_:test("from AI, admit it", function()
local circleA = {x = 0, y = 0, r = 10}
local pointP = {x = 0, y = 15}
local distance = 10
-- We find the intersection of two circles:
-- 1. circleA
-- 2. A new circle centered at pointP with radius 'distance'
local intersectionPoints = findCircleIntersection(
circleA.x, circleA.y, circleA.r,
pointP.x, pointP.y, distance
)
if intersectionPoints then
print("Found intersection points:")
for i, p in ipairs(intersectionPoints) do
print(string.format(" Point %d: x=%.2f, y=%.2f", i, p.x, p.y))
end
else
print("No points found on the circle at the specified distance.")
end
end)
The test, as it stands now, prints values that I believe:
Feature: intersections of two circles
Found intersection points:
Point 1: x=6.61, y=7.50
Point 2: x=-6.61, y=7.50
intersections of two circles, 1 Tests: Pass 1, Fail 0, Ignored 0.
I believe those values for two reasons: First, the 7.5 is the midpoint between the two input circles, and picture I drew of two equal circles makes it clear that the y coordinate will be there, and the value 6.61 looks familiar to me.
I guess I’d be wise to work this out by hand. From the diagram:
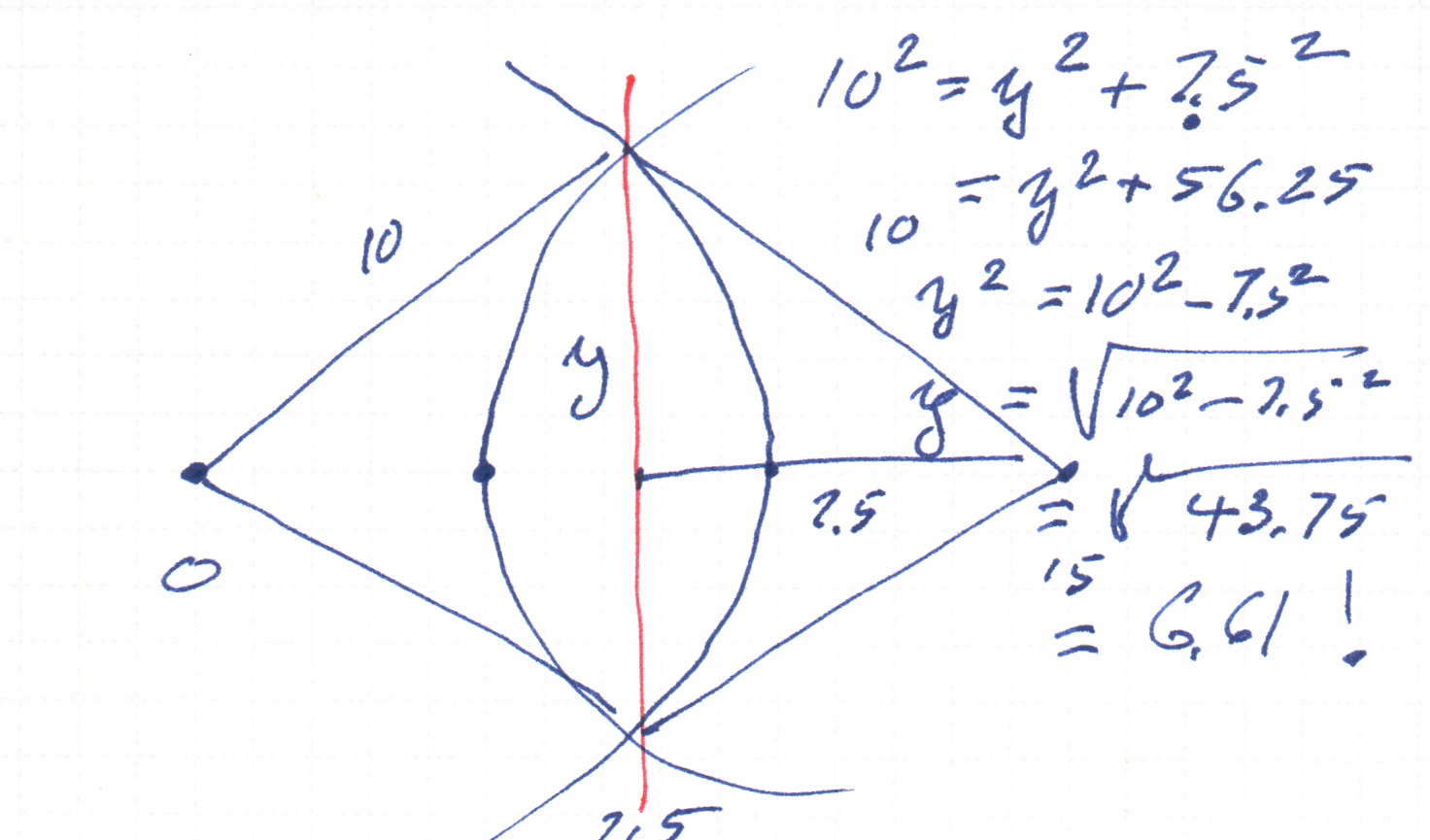
We have a right triangle with base 7.5, hypotenuse 10, and unknown altitude y. So
10^2 = y^2 + 7.5^2
= y^2 + 56.25
y^2 = 10^2 - 56.25
y = sqrt(100-56.25)
y=sqrt(43.75)
y = 6.61437 ...
So I have shown that the result is correct for these values.
Here is the rub with these “AI” solutions. If I decide to trust it, I can get back to my normal work now, converting this code to use my objects and pushing on. However, there will be code in the system that I do not understand, and that may or may not be correct. Odds are that it is correct, but playing the odds is what gets calls to customer support.
Given my standards, I am faced with two possibilities that I can live with: either figure out this code, or find an algorithm and implement it myself.
If I implement it myself, I’ll do it with TDD, and I’ll know inch by inch that it works, needing fewer hand-calculated full cases. If I try to figure it out, I’ll spend hours, will convince myself, and will leave little or no trace in the code of what I’ve learned.
The “AI” mentioned a name, Paul Bourke, and a quick search finds this page on Stack OVerflow
I think I’ll start from that It looks like the place where the google thing stole its idea.
I’ll make a new test feature and see what happens. The time is 11 AM.
At 11:33 I have worked through Bourke’s explanation here, with the aid of comments on StackOverflow. I am ready to implement, and also ready to take a break.
I would not have attained this level of understanding from reading the code. Here’s my work deriving the h angle: